Principal Component Analysis

تحلیل مولفه های اصلی(Principal Component Analysis)ابتدا در سال 1901 توسط پیرسون معرفی و پس از آن در سال 1933 توسط هتلینگ روشهای محاسباتی آن پیشنهاد شد،PCA در تعریف ریاضی یک تبدیل خطی متعامد است که داده را به دستگاه مختصات جدید برده بطوریکه بزرگترین واریانس داده ها بر روی اولین محور مختصات قرار گرفته و واریانس مرتبه بعدی بر روی دومین محور مختصات قرار می گیرد و این روند تا انتها ادامه می یابد.(شکل 1)

PCA یکی از با ارزش‌ترین نتایج کاربرد جبر خطی است که به وفور در تحلیل‌های مختلفی مانند شبکه‌های عصبی تا نمودارهای کامپیوتری استفاده شده است، چرا که یک روش آسان و ناپارامتری برای استخراج اطلاعات مرتبط از یک مجموعه داده پیچیده می‌باشد، بطوری‌که کاربرد عمده روش PCA عبارتند از :

     1- کاهش تعداد متغیرها

      2- یافتن ساختار ارتباطی بین متغیرها که در حقیقت همان دسته بندی متغیرهاست

در زندگی روزمره زمانی که می‌خواهیم اشیا و یا اجسامی را باهم مقایسه کنیم بصورت ناخودآگاه شباهت‌های آنها را کنار گذاشته و بیشتر به وجوه تمایز آنها دقت می نماییم.PCA استاندارد کاهش ابعاد را تنها از طریق پیدا کردن روابط خطی ممکن می سازد، اگر داده ها ساختارهای پیچیده‌تری داشته باشند به نحوی که نتوان آنها را بخوبی در یک زیرفضای خطی نمایش داد PCA خطی نمیتواند مفید واقع شود.  

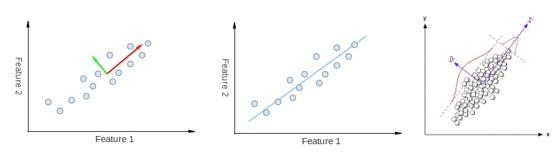
شکل 1

مفاهیم مقدماتی مورد نیاز در PCA:

فرض کنید X رشته ای از مقادیر است میانگین مقادیر از رابطه زیر بدست می آید:

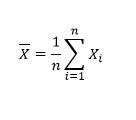
واریانس از رابطه زیر بدست می آید:

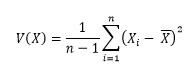
علت اینکه در رابطه فوق از عبارت n-1 بجای n استفاده شده است این است که فرض شده تمام مقادیر موجود نیست بلکه تعدادی از آنها انتخاب شده اند و در مجموعه X قرار گرفته اند، یعنی X مجموعه نمونه است نه کل داده ها، با این فرض که اگر از n-1  در رابطه فوق استفاده شود به واریانس داده های واقعی نزدیکتر خواهیم بود نسبت به این که از n استفاده شود و عیب واریانس این است که آن را حتی با خود صفت هم نمیتوان مقایسه نمود زیرا اگر فرض کنیم صفت برحسب متر است 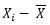هم برحسب متر است ولی 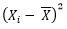برحسب مترمربع است و عمل مقایسه صحیح نیست و این یکی از معایب واریانس است، برای رفع این مسئله از جذر مثبت واریانس، انحراف معیار استفاده می شود.

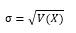
معیار هایی که در بالا ذکر شد  فقط اطلاعات مربوط به یک بعد را ارائه می کنند و دانشی را در مورد ارتباط بین ابعاد مختلف را بیان نمی کنند از این رو با استفاده از رابطه کواریانس می توان ارتباط بین ابعاد مختلف را بدست آورد، با فرض این که رشته دیگری از اعداد با نام Y وجود دارد کواریانس بین X,Y از رابطه زیر بدست می آید:

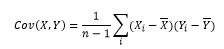
کواریانس بر حسب اینکه مثبت ویا منفی باشد نشان دهنده این است که X,Y بطور متوسط در یک جهت یا در دو جهت مخالف تغییر می کنند:

اگر Cov(x,y)>0 آنگاه X,Y مشابه هم تغییر می کنند.

اگر Cov(x,y)<0 آنگاه X,Y متضاد هم تغییر می کنند.

اگر Cov(x,y)=0 انگاه نمی توان نتیجه گرفت که X, Y مستقل هستند (بجز حالتی که X,Y هر دو نرمال باشند)

کواریانس بین تمامی ابعاد داده ها را می توان دو به دو محاسبه نمود ور در یک ماتریس ذخیره کرد که به این ماتریس، ماتریس کواریانس گویند، ماتریس کواریانس یک ماتریس مربعی متقارن است مثلا اگر سه بعد به نامهای X,Y,Z داشته باشیم ماتریس کواریانس آنها برابر است با:

علت متقارن بودن ماتریس کواریانس این است که:

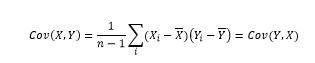
مفاهیم جبر ماتریسها

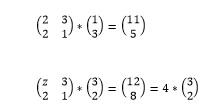
یکی از شروط ضرب دو ماتریس سازگار بودن اندازه آنها می باشد مثال:

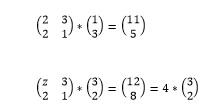
در مثال اول بردار بدست آمده مضرب صحیحی از بردار اولیه نیست، اما در مثال دوم، بردار بدست آمده چهار برابر بردار اولیه می باشد، ماتریس 2*2 که در این دو بردار ضرب کرده ایم را می توان یک ماتریس تبدیل در نظر گرفت که با ضرب آن در یک بردار می توان اندازه و راستای آن بردار را تغییر داد. در میان تمامی بردارهایی که می توان ماتریس تبدیل را در آنها ضرب نمود بردارهایی وجود دارد که پس از تبدیل راستای آنها تغییر نمی کند و فقط اندازه انها ممکن است عوض شود مانند بردار [3;2] در مثال فوق، که این بردارها، بردارهای ویژه نام دارند. بردارهای ویزه فقط برای ماتریس های مربعی معنا پیدا می کنند، یک ماتریس  می تواند دارای n بردار ویژه باشد، به منظور استاندارد کردن بردارهای ویژه، پس از یافتن بردارهای ویژه اندازه آنها را طوری می توان تغییر داد تا طول انها برابر یک شود، مثلا برای بردار [3;2] داریم

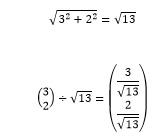
ویژگی مهم بردارهای ویژه اینست که بر هم عمودند.

الگوریتم PCA

1-انتخاب داده
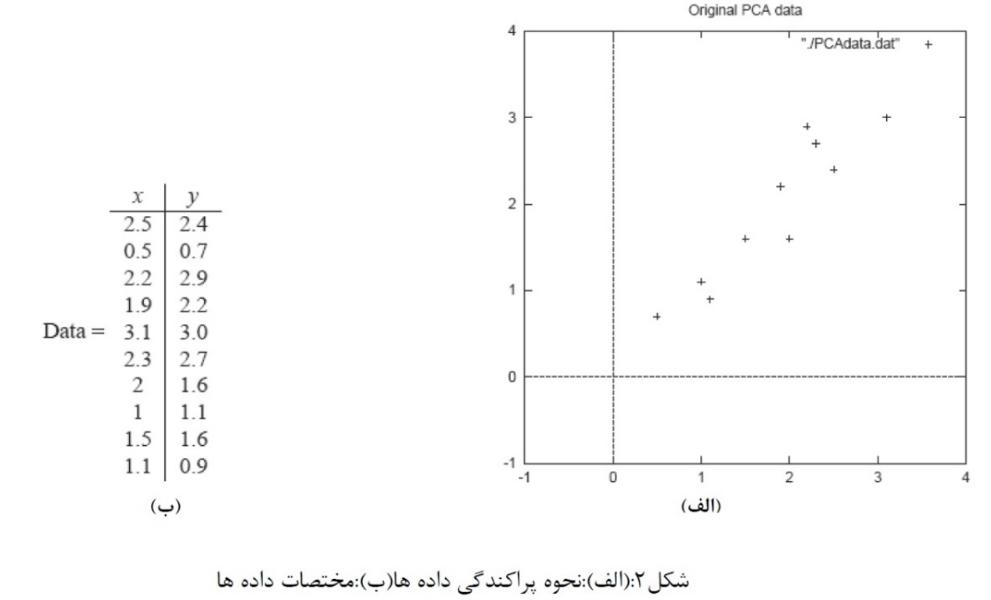
اعمال الگوریتم PCA بر روی یک مجموعه 2 بعدی داده مطابق شکل2

 

2-کم کردن میانگین از داده ها

در این مرحله، میانگین هر بعد را از مقادیر آن بعد کم می نماییم تا میانگین داده ها در هر بعد صفر شود

3-محاسبه ماتریس کواریانس

ماتریس کواریانس را به طریقی که در بالا ذکر شد برای داده ها بدست می آید

4-محاسبه بردارهای ویژه و مقادیر ویژه

5-انتخاب مولفه ها و ساخت بردار ویژگی

6-بدست آوردن داده های جدید